

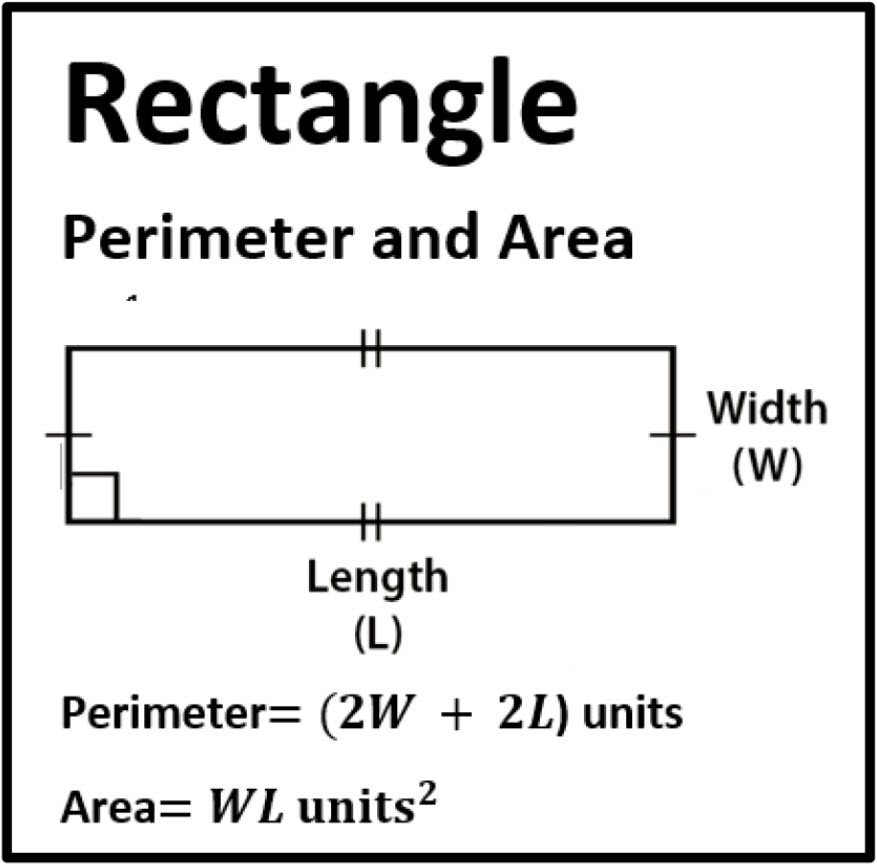
Let’s use this knowledge of area and apply it to a perimeter problem.įor example, suppose you needed to frame a large rectangular window that has an area of 35 square feet and a length of 7 feet. A rectangle that measures 3.5 cm by 4 cm would have an area of 14 cm 2 because 3.5 × 4 = 14. Remember, to calculate the area of a rectangle, we simply multiply the length by the width. In order to solve this kind of perimeter problem we need to review our understanding of area. In fact, some perimeter problems will provide you with one dimension as well the rectangle’s area. However, not all perimeter problems will provide you with the length and width in such a straightforward way. 14 + 6 + 14 + 6 would produce the correct answer, but this strategy will generally take longer, so using the formula is recommended. Using the perimeter formula saves us a bit of time by avoiding the alternative strategy which would be to add up each side length separately. Now we have P = (14 + 6) × 2, which simplifies to 40, or 40 feet. The formula states that P = (L + W) × 2, so let’s plug in 14 feet for L and 6 feet for W. For example, if the rectangle below represents a garden that needs a brick border, we can use the perimeter formula to determine how many feet of brick border we need in all. When you are given the dimensions of a rectangular shape, you can simply plug in the values of L and W into the formula in order to solve for the perimeter. The perimeter formula for a rectangle states that P = (L + W) × 2, where P represents perimeter, L represents length, and W represents width. When we calculate the perimeter, we are essentially calculating the total distance around that two-dimensional shape.Ĭalculating perimeter problems can be done in many ways, but the most efficient strategy is to simply use the perimeter formula. It can be helpful to visualize the perimeter as the fencing that surrounds a park or a backyard. Let’s remember that perimeter refers to the distance around the outside of a two-dimensional shape. Calculating the perimeter of rectangles is a helpful skill to master because it is used frequently in our daily lives. For example, we can use perimeter calculations for situations such as fencing requirements around a play field, measurements of a picture frame, distances around a walking path, or dimensions of a large window. Solving rectangular perimeter problems is a skill that has many interesting real-world applications.


 0 kommentar(er)
0 kommentar(er)
